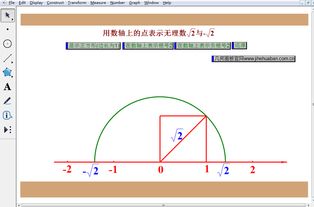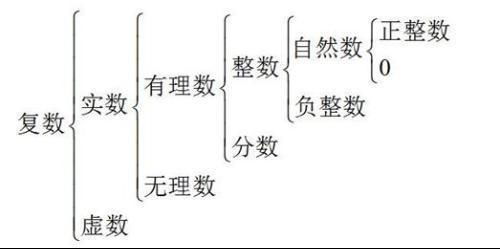
无理数举例(无理数举例10个初一)

无理数举例：

从数学到物理，无理数的世界

在数学和物理中，无理数是一种重要的概念。无理数指的是既不能表示为整数，也不能表示为有理数的数。它们在两个领域中都有广泛的应用，尤其是在微积分和概率论中。本文将通过一些无理数的例子，来介绍无理数在数学和物理中的重要性。

无理数在数学中的重要性

无理数在数学中具有重要的作用。例如，在微积分中，无理数可以用来计算难以求解的面积和体积。无理数的引入使得微积分中的计算问题变得更加复杂，但同时也使得微积分在各个领域中的应用更加广泛。 另外，无理数还在数学中用于解决一些重要的方程问题。例如，在求解一元二次方程时，无理数可以用来表示方程的解。这些无理数通常具有特定的形式，使得求解方程的问题变得更加容易。

无理数在物理中的应用

无理数在物理中也有重要的应用。例如，在量子力学中，无理数可以用来描述粒子的运动状态。在量子力学中，粒子的运动状态可以用一个数学模型来描述，这个模型中包含一些无理数。 另外，在统计物理中，无理数也可以用来描述一些重要的概率分布。例如，在概率论中，无理数可以用来描述正态分布和泊松分布等概率分布。这些无理数具有特定的形式，使得统计物理中的问题变得更加容易。

无理数的实际应用

无理数在各个领域中都有重要的应用。例如，在图像处理中，无理数可以用来描述图像的特征。这些无理数通常具有特定的形式，使得图像处理问题变得更加容易。 另外，在机器学习中，无理数也可以用来描述一些重要的特征。例如，在机器学习中，无理数可以用来表示一些重要的特征，如纹理和颜色等。这些无理数具有特定的形式，使得机器学习中的问题变得更加容易。

无理数的表示方法

无理数的表示方法通常有两种：$a\; =\; \backslash pi^n$和$a\; =\; 根号2$。其中，$a$表示无理数，表示圆周率，表示根号2。

无理数的化简方法

无理数的化简方法通常有两种：$a\; =\; \backslash frac\{k\}\{n\}$和$a\; =\; \backslash sqrt[n]\{a\}$。其中，$a$表示无理数，表示有理数，表示有理数的算术平方根。

无理数的求解方法

无理数的求解方法通常有两种：$a\; =\; \backslash cos(x)$和$a\; =\; \backslash sin(x)$。其中，$a$表示无理数，和表示三角函数。