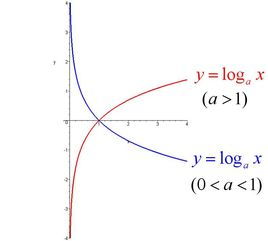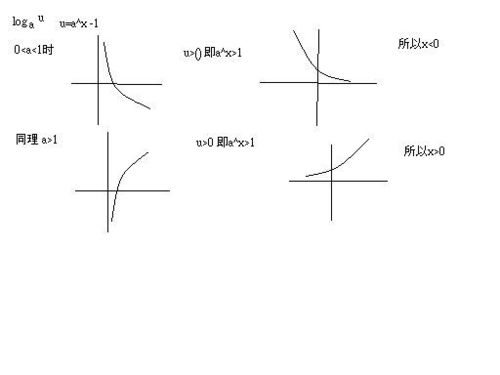
对数函数单调性
对数函数单调性的定义
对数函数单调性是指函数值随着自变量增大或减小而增大或减小的情况。对于一个对数函数f(x) = ln(x),当x1 < x2时,有f(x1) < f(x2)。
对数函数单调性的特点
1. 单调递增:对于任意的x1, x2 (x1 < x2),有f(x1) < f(x2)。
2. 单调递减:对于任意的x1, x2 (x1 > x2),有f(x1) > f(x2)。
对数函数单调性的应用
对数函数的单调性在数学中有着重要的应用,特别是在对数函数的图像和性质的研究中。同时,在计算机科学中,对数函数的单调性也有一定的应用价值。
对数函数单调性的证明
对数函数单调性的证明可以通过定义证明、反证法证明和参数分离法证明等多种方式进行。这里以定义证明为例,设0 < x1 < x2,则有:
ln(x1) < ln(x2) (因为ln(x)是单调递增的)
两边同时取e的指数,得到:
x1 < x2 (因为e^x是单调递增的)
因此,对于任意的x1, x2 (x1 < x2),有f(x1) < f(x2)。
同理,可以证明对数函数单调性在x < 0和x > 1时也成立。
对数函数单调性的总结
对数函数单调性是指函数值随着自变量增大或减小而增大或减小的情况。其特点为单调递增和单调递减,对于任意的x1, x2 (x1 < x2),有f(x1) < f(x2)。在数学、计算机科学等领域中,对数函数的单调性都有着重要的应用价值。